Logiske modeller for et utvalg av oppgavene til kapittel 7 (det kan bli aktuelt å legge til flere).
Uten avgiftsbeløp:

Med avgiftsbeløp:
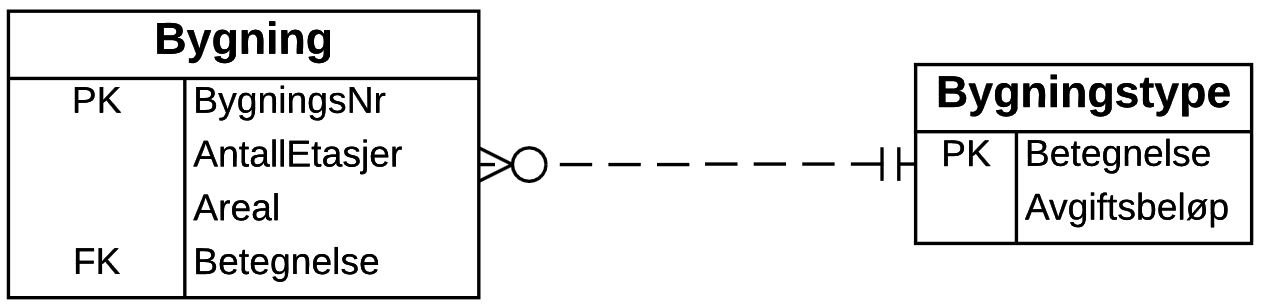
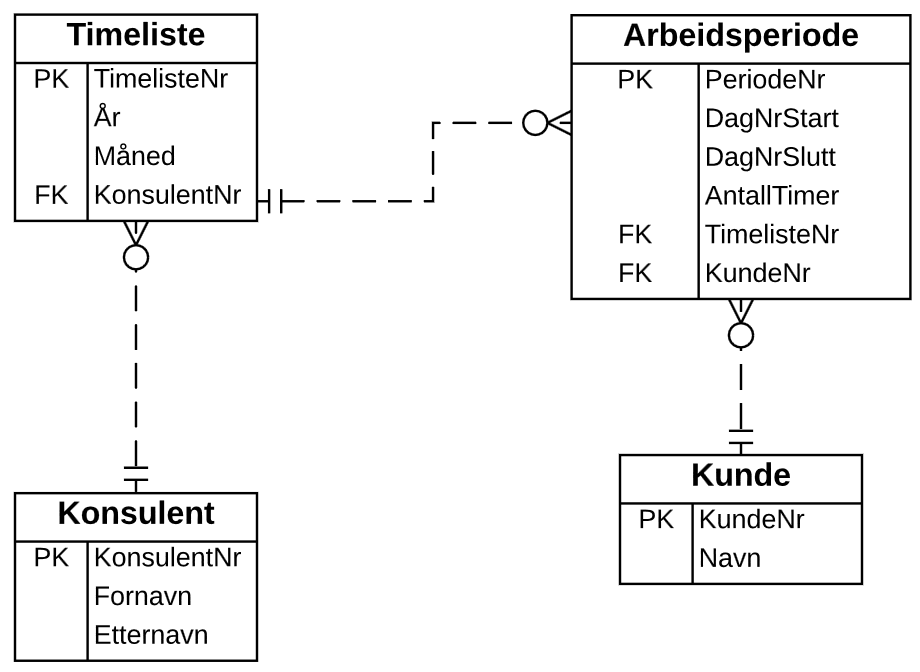
En komponent kan kun inngå i ett bestemt produkt:
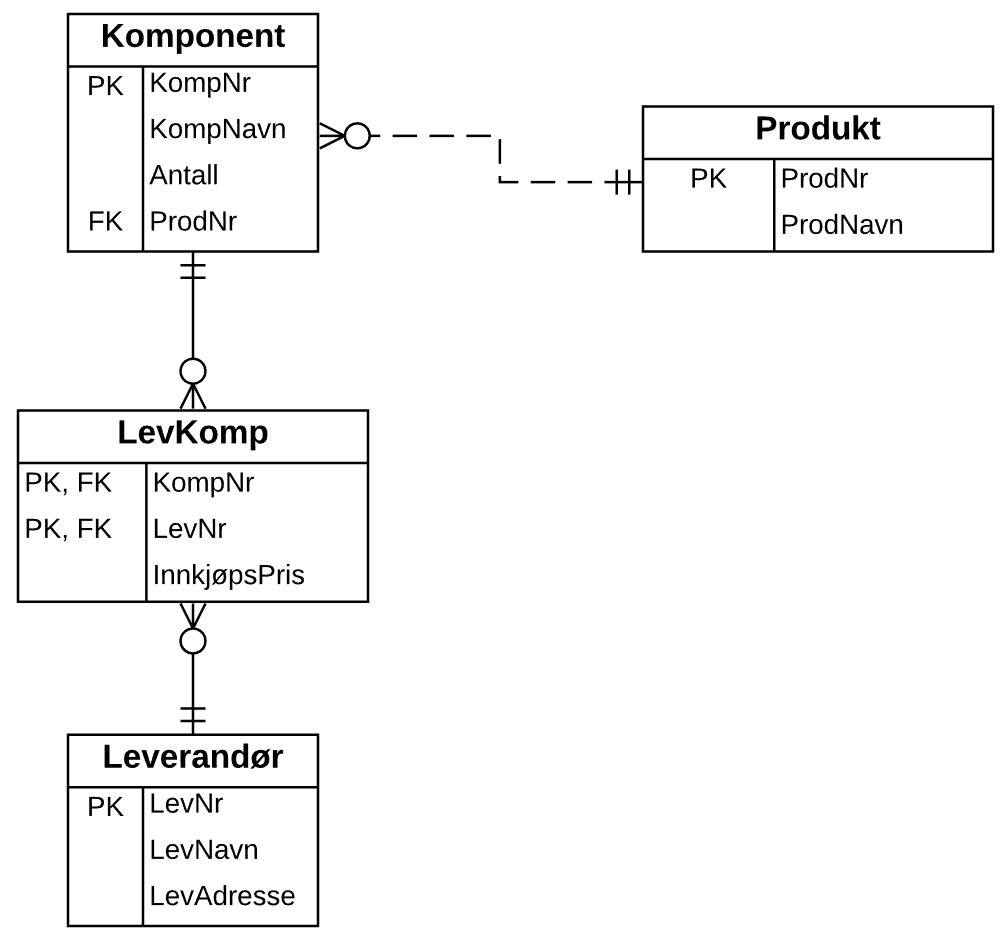
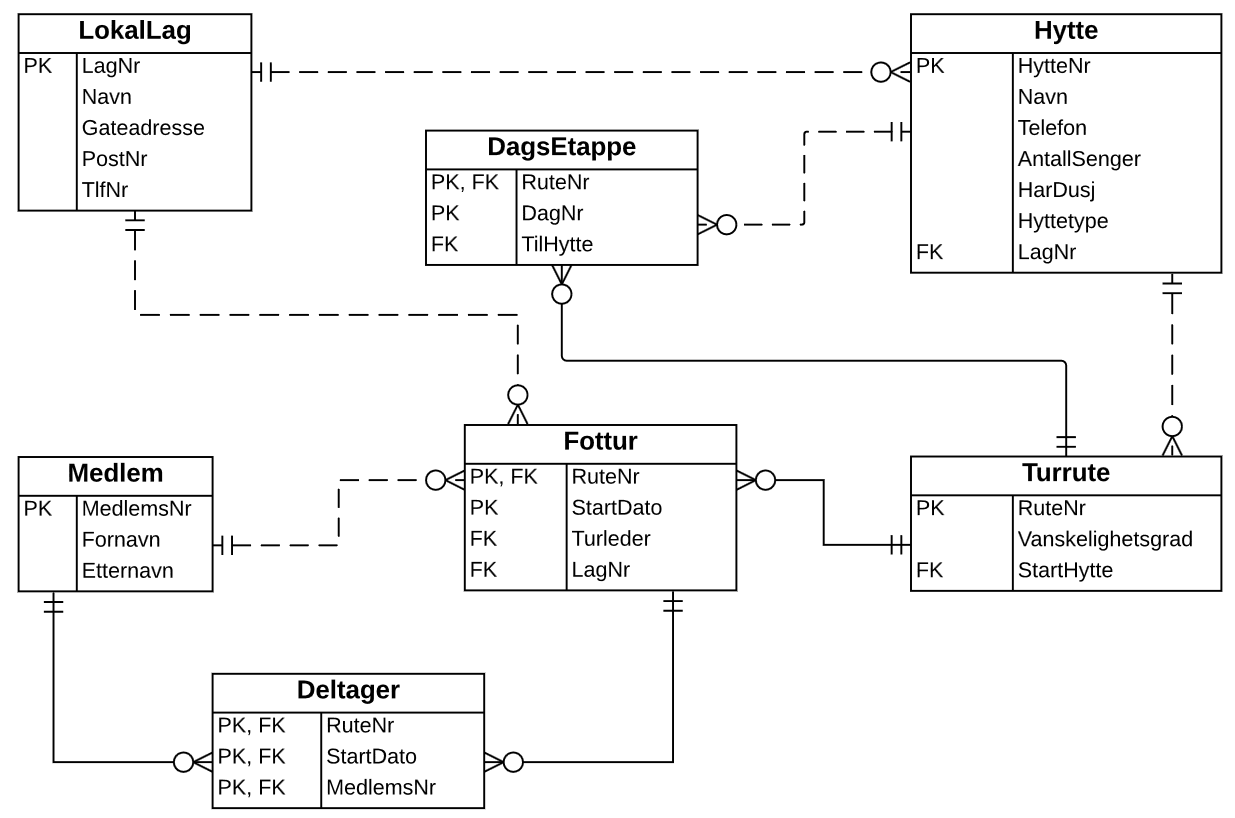
Vi får en tabell for hver entitet, og dessuten en tabell for mange-til-mange forholdet mellom Medlem og Fottur.
Merk at både Turrute.StartHytte og Dagsetappe.TilHytte er fremmednøkler mot Hytte, og dermed inneholder et hyttenummer. Dette er eksempler på at fremmednøkler ikke nødvendigvis har samme navn som tilhørende primærnøkkel.
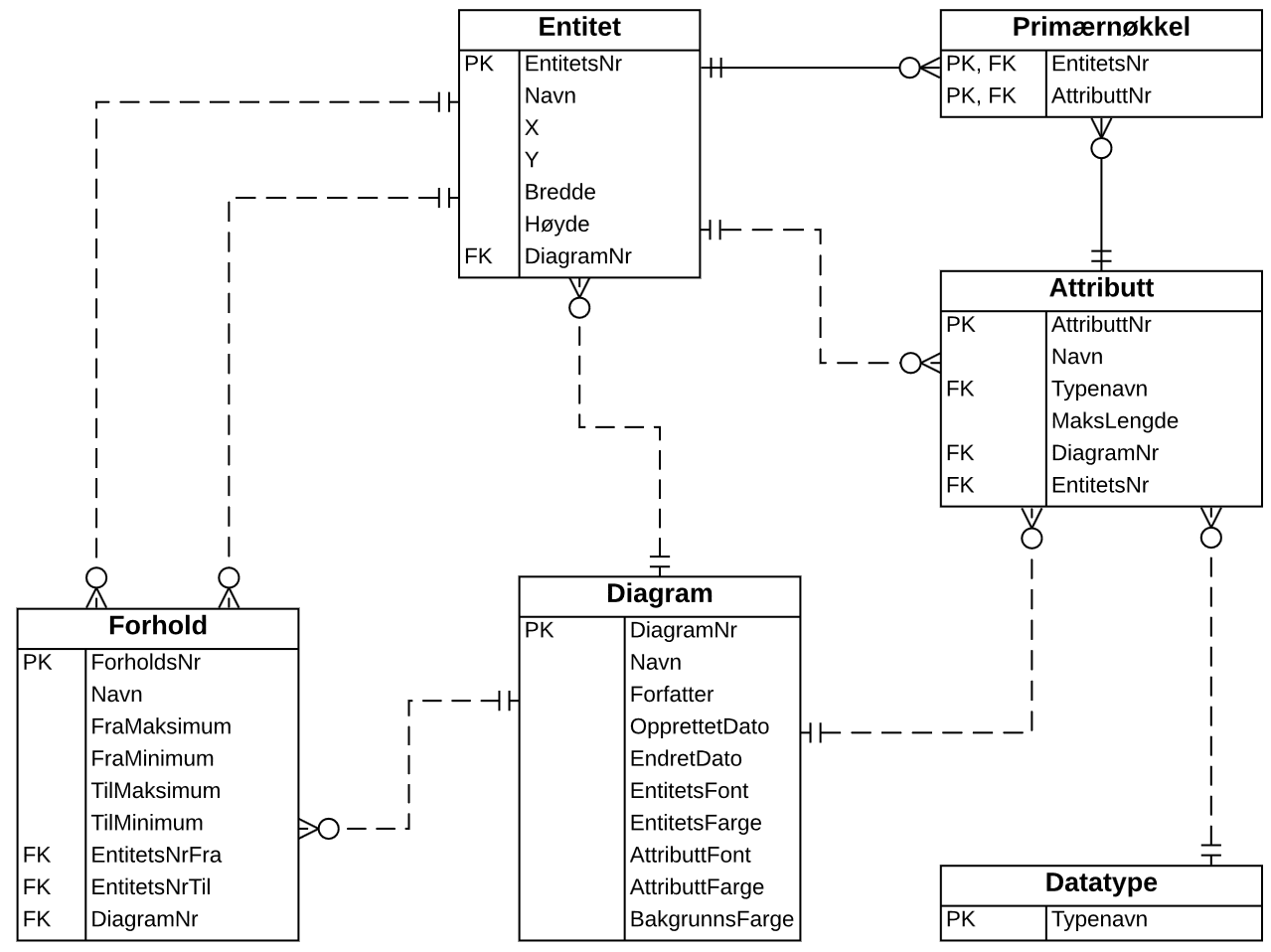
Romreservasjonssystem.
Tabellstruktur:
Utlån av bøker og CD-plater.
Her skulle man utføre "reverse engineering", altså bygge en datamodell fra en database. Vi kan starte med å tegne en logisk datamodell, som bare er en visualisering av tabellstrukturen:
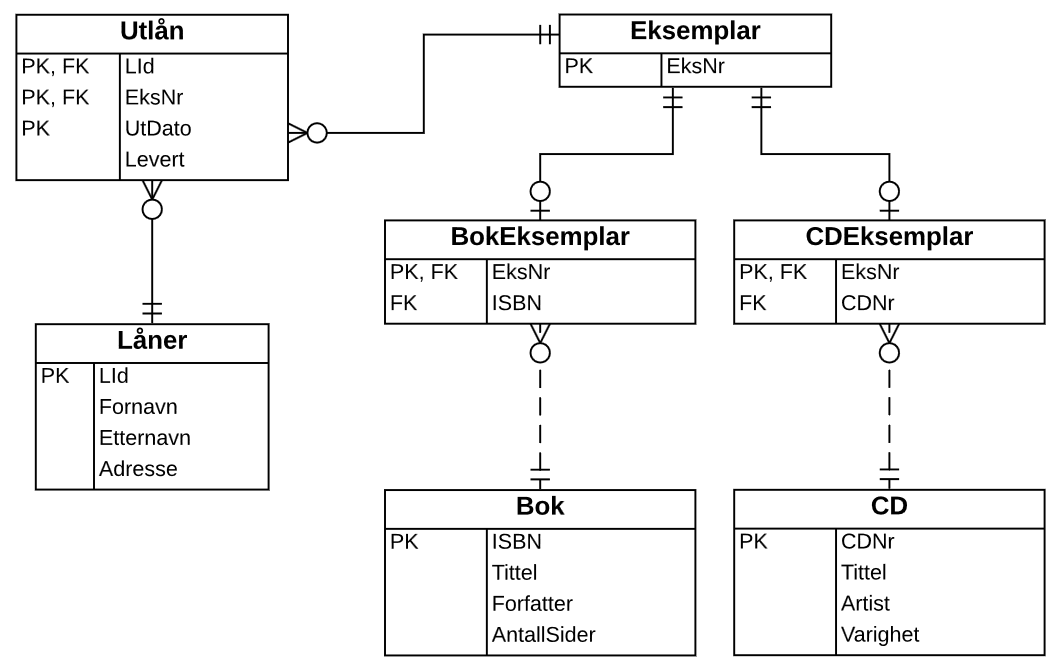
Så kan vi fjerne fremmednøklene og få tilsvarende begrepsmessige datamodell (under). Forholdet mellom Eksemplar og de to entitetene BokEksemplar og CDEksemplar kan gjerne uttrykkes med subtypeforhold, se avsnitt 7.6.4.
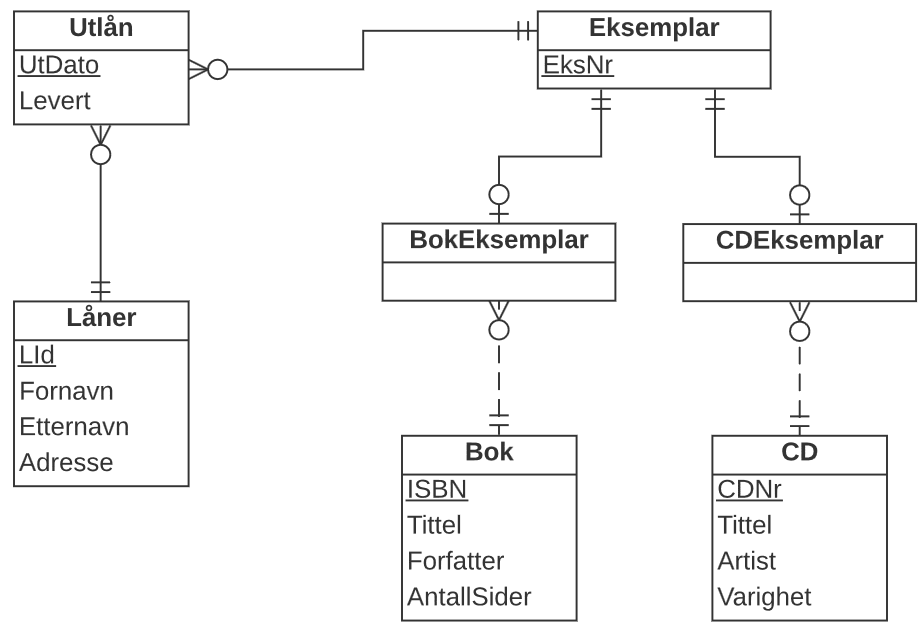
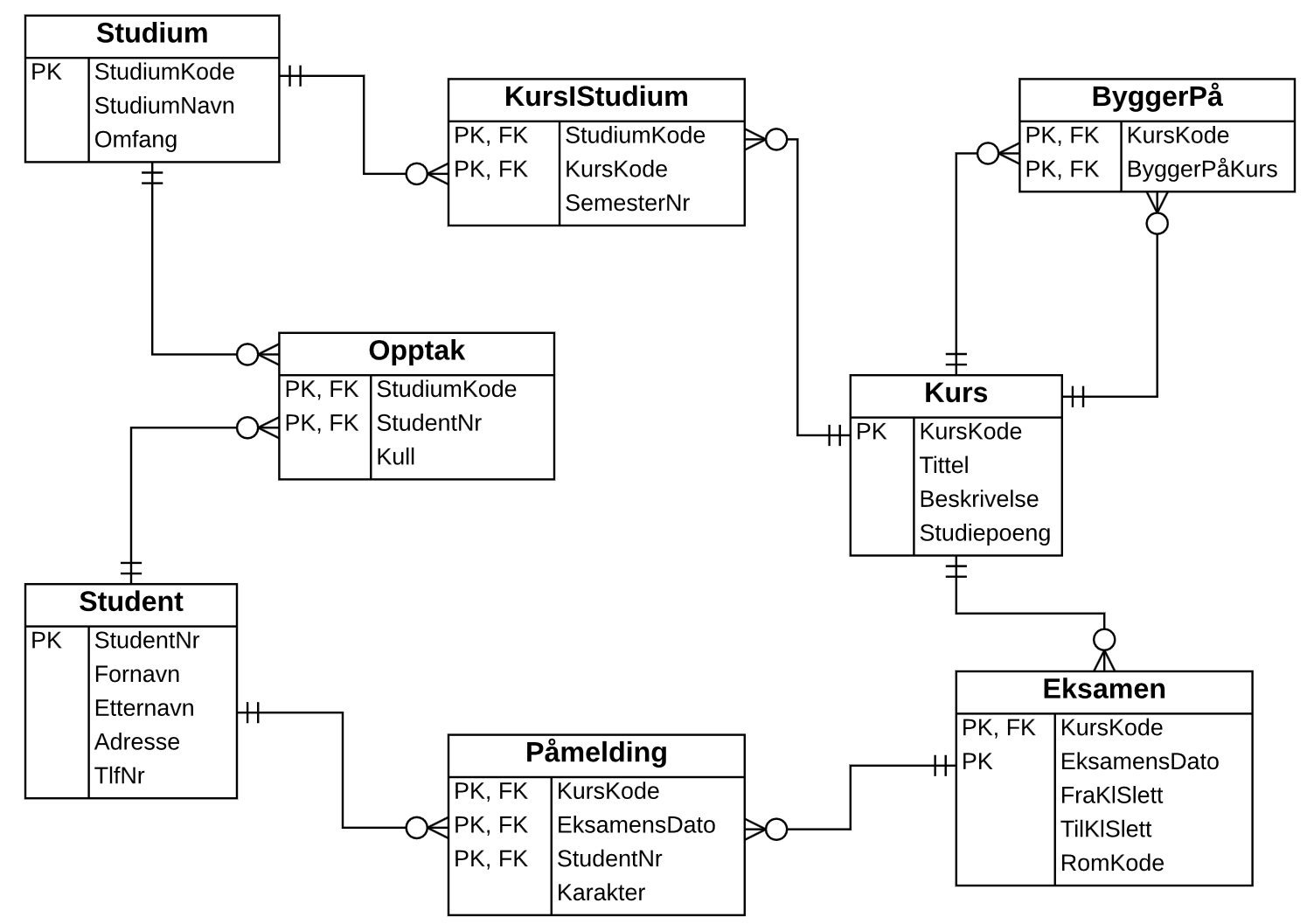
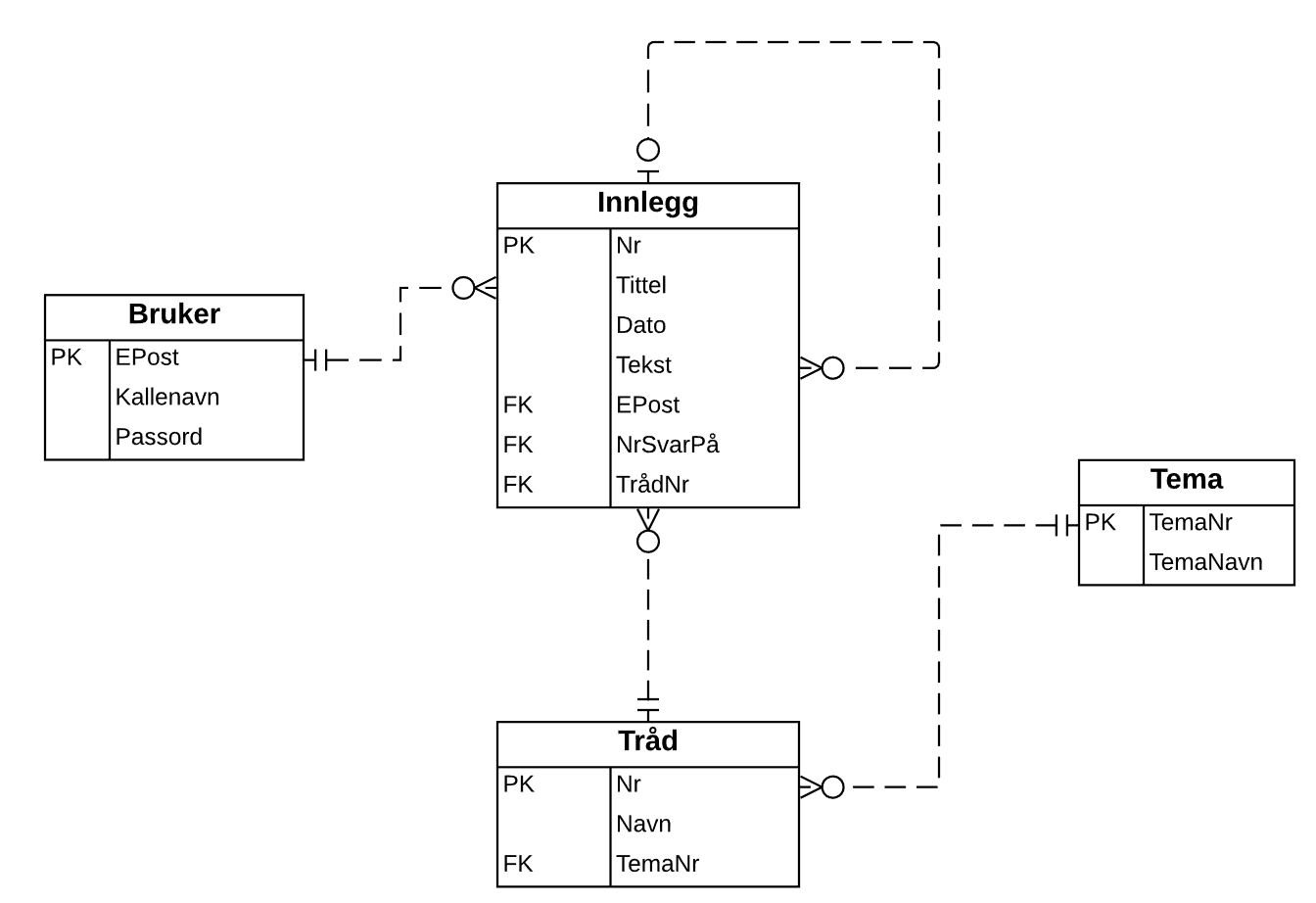
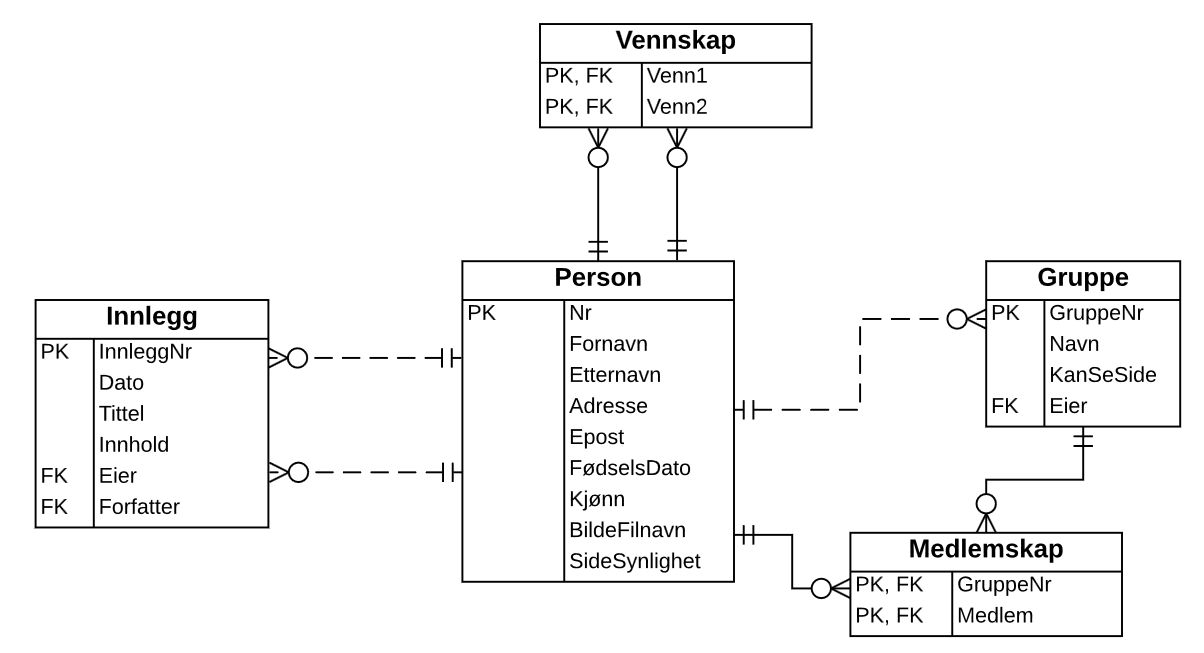
Støttesystem for nettbasert undervisning.
Begrepsmessig datamodell:
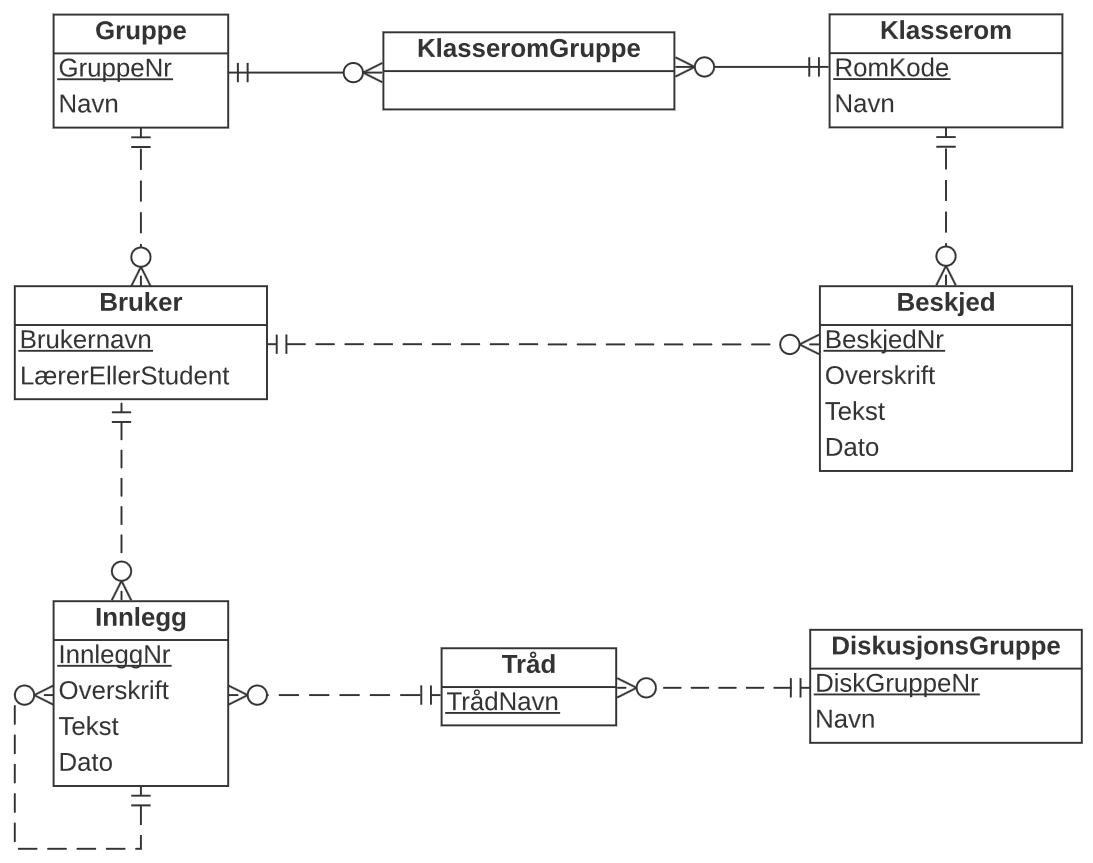
Logisk tabellstruktur:
Kort forklaring til noen av tabellene/kolonnene:
Konfirmasjon.
Første observasjon bør være at kirkeboka begrenset til konfirmasjon vil inneholde maksimalt én innførsel pr konfirmant. Fra antakelsen om at ingen personer har samme navn kan vi slutte at konfirmantens fornavn og etternavn sammen utgjør en kandidatnøkkel for tabellen (det er altså en funksjonell avhengighet fra disse to til alle andre kolonner).
Andre funksjonelle avhengigheter, der navn på konfirmant, far og mor er døpt om til FarFornavn, FarEtternavn og tilsvarende:
Hvert normaliseringssteg tar tak i en funksjonell avhengighet, skiller ut involverte kolonner i en egen tabell, og lar kun determinantene stå igjen i "utgangstabellen". Hvis dette gjøres for alle avhengighetene over - bortsett fra avhengighetene fra kandidatnøkkelen - får vi følgende tabellstruktur, der passende tabellnavn er påført:
Disse tabellene er alle på BCNF, og vi er ferdige med normalisering.
Selv om normalisering fjerner redundans, er det en mekanisk prosess som med fordel bør kombineres med "sunn fornuft". Vi ser at både far og mor er personer, og slår disse tabellene sammen til en. En ytterligere observasjon er at konfirmantens fødselsdato og fødested også kan legges i persontabellen. Til slutt endrer vi navnet på kolonnen KonfDato i tabellene for bosted/sivilstand til det mer nøytrale Dato. Da får vi:
I en virkelig løsning vil det være naturlig å identifisere personer ved et personnummer, slik:
Kolonnene KonfSted, Fødested og Bosted vil trolig være fremmednøkler mot en Sted-tabell. Hvis vi skal ta vare på adresser fra flere kommuner, er ikke adresse entydig - vi trenger kanskje både adresse og postnummer. I så fall vil KonfSted, Fødested og Bosted være sammensatte fremmednøkler (består av både adresse og postnummer).
Bomstasjoner.
Oppgaveteksten antyder at et registreringsnummer identifiserer en bil (og dermed et bilmerke). Vi velger her å anta at dette gjelder, selv om det i praksis er mulig å gjenbruke et registreringsnummer på en annen bil.
Oppgaveteksten antyder også at en bil kun har én eier, og at et bomstasjonsnummer identifiserer kommunen der bomstasjonen er plassert.
En bil (et registreringsnummer) kan ikke bli observert på flere steder (bomstasjoner) samtidig, så RegNr + Dato + KlSlett bestemmer StNr. Her tenker vi oss at KlSlett måler tiden så nøyaktig at det ikke er mulig for en bil å passere to ganger på "samme tidspunkt".
Hvis vi legger dette til grunn får vi følgende funksjonelle avhengigheter:
Kandidatnøkkel blir RegNr+Dato+KlSlett, og normalisering gir følgende resultat:
Flervalgsprøver.
Primærnøkkel er TestNr + SpNr + AltNr + Bruker. Tabellen inneholder partielle avhengigheter og er dermed på 1NF.
Behandler TestNr → TestNavn:
Behandler TestNr+SpNr → SpTekst og TestNr+SpNr → Korrekt for tabell Flervalg1:
Behandler TestNr+SpNr + AltNr → AltTekst for tabell Flervalg2:
Behandler TestNr+SpNr + Bruker → Svar for tabell Flervalg3:
Flervalg4 inneholder to flerverdiavhengigheter TestNr + SpNr + AltNr => Bruker og TestNr + SpNr + Bruker => AltNr. Vi splitter denne tabellen:
Vi observerer at Flervalg5 er "inkludert" i Alternativ og at Flervalg6 er "inkludert" i Svar. Sluttresultatet blir dermed:
Normalisering av T(A,B,C,D,E).
Gitt tabell T(A,B,C,D,E) med funksjonelle avhengigheter A→B, C→D og C→E. A og C er kandidatnøkkel siden de sammen bestemmer alle andre kolonner. Vi har flere partielle avhengigheter. Dette er et brudd på 2NF, så tabellen er på 1NF. Vi splitter T i to tabeller:
T2 har C som kandidatnøkkel og er på BCNF. I T1 så er A+C kandidatnøkkel. A→B er en partiell avhengighet, så T1 er på 1NF. Vi splitter T1:
Både T11 og T12 er på BCNF (om ikke annet så fordi de har kun to kolonner). I T12 så er A kandidatnøkkel.
Sluttresultatet består av T2, T11 og T12.
Følgende tabell er et eksempel på hva den opprinnelige tabellen kan inneholde:
Resultatet blir, hvis vi omnavner T11, T12 og T2 til henholdsvis ProsjektDeltakelse, Prosjekt og Ansatt:
Normalisering av T(A,B,C,D).
Gitt T(A,B,C,D) der A→ B, B→C og C→D.
A→ B og B→C gir A→ C. A→ C og C→D gir A→D. Dermed er A kandidatnøkkel. B→C og C→D gir begge transitive avhengigheter, så T er på 2NF. Vi splitter med hensyn på C→D
T2 er på BCNF. T1 splittes med hensyn på B→C:
Sluttresultatet består av T11, T12 og T2.
Normalisering av T(A,B,C,D,E).
Gitt T(A,B,C,D,E) der A,B→C, B→A, B→D og D→E.
A,B→C og B→A gir B→C. B→D og D→E gir B→E, så B er kandidatnøkkel. D→E gir en transitiv avhengighet, så T er på 2NF. Vi splitter med hensyn på D→E:
Begge tabeller er på BCNF.
Normalisering av T(A,B,C,D,E).
Gitt tabell T(A,B,C,D,E) uten funksjonelle avhengigheter. Hvis det ikke finnes funksjonelle avhengigheter må nødvendigvis alle kolonner være med i kandidatnøkkelen (det er alltid slik at kolonner som ikke blir bestemt av noen andre kolonner må være med i kandidatnøkkelen).
Koblingstabeller uten andre kolonner enn primærnøklene fra "hver side" gir denne typen tabeller. Eksempel (riktig nok med litt færre kolonner):
Normalisering av "symbolske" tabeller.
For å "oppdage" de funksjonelle avhengighetene må vi kjenne til hva de ulike kolonnene "betyr". Når vi for eksempel sier at AnsNr→Etternavn må vi vite at det ikke finnes to ansatte med samme ansattnummer. Dette krever kunnskap om hva AnsNr og Etternavn er. Når vi først har klarlagt de funksjonelle avhengighetene, er selve normaliseringen styrt av "formelle regler".
Normaliserte tabeller for ansatt-data.
Normaliserte tabeller for bil-reservasjoner.
Rekkefølge.
Rekkefølge kan spille en rolle. Betrakt T(A,B,C,D) med avhengigheter A→B, B→C og C→D. A er kandidatnøkkel. Fra B→C og C→D får vi B→D. Normalisering der vi først behandler C→D og deretter B→C gir følgende tabeller på BCNF:
Se hva som skjer hvis vi starter med B→D:
S1 splittes videre med hensyn på B→C:
S11, S12 og S2 er på BCNF, men avhengigheten C→D involverer nå to tabeller. Vi ser imidlertid at S12 og S2 begge har B som kandidatnøkkel, så de bør slås sammen:
S3 splittes så med hensyn på C→D
Tabellene S11, S31 og S32 har samme struktur som T1, T2 og T3. Tommelfingerregel: Hvis B→C og C→D (og dermed B→D), behandle C→D før B→D. Eller behandle B→C og B→D sammen, fordi de har samme determinant.
Eksempel på BCNF-brudd.
Naturlig eksempel på en tabell som er på 3NF, men ikke på BCNF:
LærerId, Klasse→AntallTimer, RomNr, slik at LærerId+Klasse er kandidatnøkkel, og dessuten gjelder RomNr→Klasse (hver klasse har sitt eget klasserom).
Hvor "naturlig" eksemplet er kan diskuteres, på de fleste skoler vil det være noen rom som brukes av flere klasser (musikkrom, datarom m. fl.) - her ser vi på en skole med kun "klasserom".
Flyavganger
Idéen er å innføre en boolsk (ja/nei) kolonne for hver ukedag som sier om flyruten har avgang denne dagen: